Everything You Need to Know to Pass the Geometry Regents
If you lot're currently attending a public high schoolhouse in the state of New York, then you lot'll need to laissez passer the New York Regents exams in society to go your diploma. The Geometry Regents examination tests you on a huge array of geometry-related topics, from angles to 3-D shapes. The upcoming Geometry Regents exam is on Wednesday, January 22, 2020, at ix:15 am. This all-encompassing Geometry Regents review guide will tell you everything you demand to know near the format of the exam, what information technology tests y'all on, and what questions look like. We'll too give you lot our best tips for acing it. Let's kickoff off our Geometry Regents review past looking at the structure of the math test. Geometry Regents is a four-part exam consisting of 35 questions, and yous'll have three hours to consummate it. Here'due south an overview of the format: Each multiple-choice question has four answer choices (labeled 1-4) from which you will choose one and then record information technology on a dissever reply sheet. For the constructed-response questions, yous must practise the post-obit in order to earn total credit, per the official Geometry Regents instructions: "Conspicuously indicate the necessary steps, including appropriate formula substitutions, diagrams, graphs, charts, etc. Utilize the data provided for each question to determine your answer. Note that diagrams are not necessarily fatigued to scale." Essentially, you lot've got to show your piece of work. Putting downwardly only a correct respond volition cyberspace you one point, simply that's it. While yous won't become divide scrap newspaper for the exam, you may utilise any blank spaces provided in the exam booklet (though it will not be scored). Notation that you will exist given one sheet of fleck graph newspaper (should you choose to apply it) at the back of the test booklet; anything written on this will non be scored. The following tools and devices must exist bachelor for you to utilise on the Geometry Regents exam: Finally, you'll get a "Loftier School Math Reference Sheet" with basic formulas and conversions that could come in handy during the exam. This reference sheet tin exist plant at the back of your test booklet; you may tear information technology out along the perforated edges and use at any time during the Geometry Regents examination. Here'due south how the reference sail will appear: Each of the four parts of Geometry Regents contains different types of math questions: Let's take a look at examples of these below. All questions come up from the August 2019 assistants of the Geometry Regents test, and all educatee responses come from NYSED Regents. This question is substantially asking y'all to do two things: Nosotros know it'south request united states of america to notice the volume because it gives us the weight of the golf brawl per cubic inch. (Whenever you hear the give-and-take "cubic," it's likely going to exist a book-related problem!) To notice the volume of a sphere, you must know the post-obit formula (which is fortunately on the reference sheet above, so you don't need to memorize it): $V={four/iii}π{r^3}$ In this formula, $V$ stands for "book" and $r$ stands for "radius," which is equal to half the bore of a circle or sphere. We're told that the diameter of the golf ball is 1.680 inches. Dissever this number in half to go the radius: $1.680/ii=0.84$ Now, we tin can plug this number into our book formula and solve: $V={4/3}π{0.84^3}$ The book of the golf brawl is roughly 2.484 cubic inches. Merely this problem isn't asking for the book—it's request for the weight of the ball. We already know that one cubic inch weighs 0.6523 ounces, and then all nosotros need to do is multiply this by the total number of cubic inches, i.east., the book we found above: $two.484*0.6523=one.62$ This gives us 1.62 full ounces, which is the same every bit answer option 2. In that location are some cardinal rules about angles y'all'll demand to know in gild to solve this problem: We've been asked to find the measure out of angle $∠ B$. First things beginning: you lot likely noticed that the line from angle $∠ A$ to angle $∠ C$ that divides the parallelogram has created two triangles, the left of which already has ii angles filled out for us: $98°$ and $36°$. To discover angle $∠ D$—the last angle in that triangle—we demand to subtract the measures of the other ii angles ($\bo 98°$ and $\bo 36°$) from $\bo 180°$, since all angles in a triangle must add together upward to $180°$: $98+36=134$ Considering opposite angles are congruent in parallelograms, nosotros can conclude that $∠ \bi D= ∠ \bi B$, pregnant that $∠ \bi B$ must also equal $\bo 46°$. You would demand to show your thinking clearly in order to get total credit for this. Below is a sample student response that approaches the problem a little differently but nonetheless gets the right answer and earns total points: To solve this problem, think of the cargo trailer as two separate shapes: Nosotros need to notice the full volume of the trailer, so we should get-go past finding the volume of the rectangular prism. To discover the volume of a rectangular prism, yous just multiply the length, width, and summit: $V=(ten)(vi)(6.five)$ We know that the volume of the rectangular function of the cargo trailer is equal to 390 cubic feet. But what about the triangular function? The easiest way to notice the book of a triangular prism is to solve for the surface area of the triangle first and then multiply it by the top (which nosotros know is six.five ft). To detect the area of a triangle, nosotros must use the following formula (which is on the reference canvass): $A={one/2}bh$ Think of the triangle as if information technology's been turned on its side. In this formula, $b$ is the "base" of the triangle (the vertical dotted line) and $h$ is the "elevation" (the horizontal dotted line). Note that the elevation we are talking about here is not the height of the cargo trailer, which is 6.five ft! Because the base of the triangle is as well one side of the rectangle, we know that the measurement of this side has to be 6 ft (like its reverse side). At present, we just have to find the top of the triangle. To do this, divide it into two right triangles using the dotted height line; this causes the base to divide in half as well, giving us 1 right triangle with a base of iii and a hypotenuse of iv. We'll call the unknown measurement (the superlative of our original triangle) $x$. To detect $10$, we can use the Pythagorean theorem (on the reference sheet): $a^2+b^2=c^2$ Plug the numbers we accept for our base of operations (3) and the hypotenuse (4) into the formula to solve for $ten$: $(3^2)+x^2=iv^two$ Since we at present have the height, we can go back and solve for the area of our original triangle using the original base of operations (six) and plugging everything into the triangle area formula: $A={1/2}bh$ Now, multiply the surface area of the triangle past the summit of the trailer (6.v ft) to go the volume of this section of the trailer: $V=(6.5)(7.9374)$ Finally, add the 2 volumes together to get the total book of the trailer: $V=51.5931+390$ Our reply, rounded to the nearest cubic foot, is 442 cubic anxiety. Here's a sample student response that earned full credit: This 3-office question is worth a whopping 6 credits. Let'due south look at how nosotros'll need to approach it, i department at a time. Given three sets of coordinates for each point on the triangle $ABC$, we must determine whether this triangle is isosceles (in other words, does it accept two sides that are equal in length?). Nosotros can figure out the lengths between $A$, $B$, and $C$ using the distance formula (which is not on your reference sheet). To observe the altitude between points ($x_1$, $y_1$) and ($x_2$, $y_2$), we utilise this formula: $√{(x_2-x_1)^2+(y_2-y_1)^2}$ Permit's use the points $A$ and $B$ first to find the distance of side $\ov {AB}$. Indicate $A$ is located at $(1, 2)$ and point $B$ is located at $(-5, three)$: $√{(-five-1)^2+(three-two)^2}$ The length of side $\ov {AB}$ is $\bo √{37}$. Now, let's solve for the length of side $\ov {BC}$. Remember that $B$ is at $(-five, 3)$ and $C$ is at $(-vi, -three)$: $√{(-half dozen--v)^2+(-three-3)^2}$ The length of side $\ov {BC}$ is besides $\bo √{37}$, so we tin say that triangle $ABC$ is isosceles. Here's how one student wrote this out to earn full credit: This part isn't besides tricky if you utilize the set of axes to graph out the triangle and foursquare. Here'southward ane pupil's correctly graphed diagram: You tin can run across hither that the pupil first started by graphing out the triangle and connecting points $A$, $B$, and $C$. Because opposite sides are parallel in a foursquare, we can observe signal $\bi D$ by drawing a bottom line that's parallel to $\ov {BA}$ and a vertical line that'south parallel to $\ov {BC}$. In other words, to observe point $D$ (and to brand side $\ov {CD}$), all you lot demand to exercise is copy the gradient of $\ov {BA}$ by counting to the right half dozen units and down 1 unit of measurement. (Or, you could find side $\ov {AD}$ first by copying the slope of side $\ov {BC}$ and counting to the left 1 unit and downwards 6 units.) Both methods should yield the correct outcome: D = (0, -4). The terminal part of this question is to prove that the quadrilateral above with the coordinates $(0, -four)$ for $D$ is, in fact, a square. Nosotros know that a square has 4 equal sides, and so nosotros must show that sides $\ov {Advertizement}$ and $\ov {CD}$ equal $√{37}$ (the same length for sides $\ov {AB}$ and $\ov {BC}$). To do this, just plug these coordinates into the distance formula and solve. Call up that point $A$ is $(one, 2)$, $C$ is $(-6, -three)$, and $D$ is $(0, -4)$: $\ov {AD}=√{(0-i)^ii+(-four-2)^2}$ $\ov {CD}=√{(0--6)^2+(-4--iii)^two}$ This lone won't become you full credit, though—you must also evidence that the slopes of consecutive sides in a foursquare are opposite reciprocals (pregnant that a number is flipped upside down into a fraction with the opposite sign). Doing this proves that consecutive sides are perpendicular to each other, thereby forming right angles—an essential feature of a foursquare. To prove that the slopes are opposite reciprocals, find the gradient of two perpendicular sides (east.thou., $\ov {AB}$ and $\ov {BC}$) using the slope formula (which is not on your reference sail): $\Slope={y_2-y_1}/{x_2-x_1}$ Here are the slopes of $\ov {AB}$ and $\ov {BC}$ using their provided coordinates: $\Slope \of$ $\ov {AB}={3-2}/{-5-1}$ $\Slope \of$ $\ov {BC}={-three-3}/{-6--5}$ ${-1/6}$ is the opposite reciprocal of half-dozen, proving that $\ov {AB}$ and $\ov {BC}$ are perpendicular to each other and that $∠ B$ is a right angle. Hither's a pupil'southward answer to bear witness you how you could write this out: Now, what percentage of Geometry Regents does each topic accept upwardly? Refer to the chart below: Source: Engage NY via the New York Country Didactics Department If you're taking the Geometry Regents exam to fulfill your high schoolhouse graduation requirements, it'southward incredibly of import that y'all pass it. Passing means scoring at least 65, or earning virtually 29-30 credits/points. You can utilise the official Geometry Regents raw score conversion charts to see how points generally translate into last scaled scores on the test. Each year differs slightly, and so it volition never be the exact same number of credits y'all need. Hither are five tips to assistance y'all get this passing score on test solar day. One of the all-time ways to do some Geometry Regents review is to take official practice tests, which you tin can find and download for gratis on the New York Country Education Department website. These are real, previously administered exams, and so you can rest assured you'll be getting authentic and realistic test-taking practice when y'all use them. It's all-time to take one exercise exam at the get-go of your prep, one around the centre, and i close to test twenty-four hour period. This style you can see your progress and get a sense for what topics or question types are giving y'all the most problem. Make sure to time yourself as you would on the real test (3 hours) and have out a graphing estimator, ruler, and compass. Yous should also have the test in a tranquillity room, away from other people, then y'all can focus ameliorate and go used to real testing weather. One time you're finished, score your test with its answer key to see how well y'all did and whether yous passed with a scaled score of 65 or higher. Refer to the model student responses so yous can meet how sure math problems are supposed to be solved, besides equally what types of answers earn (and don't earn) full credit. Everything that's tested on the Geometry Regents exam is stuff yous should have already learned in your high school geometry class. Therefore, yous tin can use your onetime homework assignments, graded quizzes and tests, and geometry textbook to review the concepts tested on the examination. Look for patterns in your mistakes to see whether there are any major areas y'all're still struggling to sympathise conceptually. If yous're looking for practice questions, run across whether your geometry textbook has whatever you lot didn't practice for in-course practice or homework assignments. Your geometry teacher wants you lot to pass Geometry Regents (bold that'due south the math test you're choosing to take for your loftier school diploma), and then don't be afraid to ask them for aid with any concepts or areas you're having problems with. You could also talk to your instructor near what a total-credit respond should look like for the trickier constructed-response questions. Although Part I has more questions than any other part on Geometry Regents, it's critical that you lot save your time for the constructed-response questions in Parts II, Three, and IV, since these are worth more than credits and require y'all to show your piece of work. You'll have 3 hours in total for the examination, simply you don't want to waste the majority of that time on the first (and arguably easiest) function, so attempt to spend no more than an hr on Part I. This will requite you a total two hours for Parts II, Iii, and Four (and ideally some leftover time you can use to check your piece of work at the stop). An hour on Function I comes out to about two and a one-half minutes per question, making this a solid pace to aim for. At that place's no guessing penalty on Geometry Regents, so you should put down an respond for every question on the exam, even if y'all have no thought how to solve information technology. For multiple-choice questions, utilise the process of elimination first to see if you tin can go rid of one or two obvious wrong answers. This style yous'll raise your chances of guessing the correct answer from 25% to 33% or even l%! You might besides desire to come up up with a guessing number (1-4), which you will cull whenever you don't know which respond pick to pick. For instance, if your guessing number is 2, then y'all'd always choose answer choice 2 for whatsoever multiple-pick questions you didn't know how to solve. For the constructed-response questions, endeavor to solve as much of the problem as you can. Fifty-fifty if all you know is the first step in a problem, write it down—Parts 3 and 4 can give you lot partial credit for showing your piece of work, even if it'due south incomplete, and so it's always worth putting down something! The Geometry Regents test is one of three math Regents tests that students at public loftier schools in New York tin can choose from as office of their graduation requirements. The examination consists of 35 questions spread across four parts, including a multiple-choice section and three constructed-response sections, which are worth anywhere from 2 to 6 credits per question. A passing score is 65, equal to near 29-30 credits. Geometry Regents covers a wide range of geometry topics, from polygons, circles, and triangles to angles, reflections, and 3-D shapes. The easiest way to make sure you pass this test is to take real Geometry Regents tests from by administrations, review notes and materials from your geometry class, and inquire your geometry or math instructor for guidance. On test mean solar day, be sure to respond every question, use the process of elimination as needed for trickier questions, and save virtually of your time for the hardest parts of the exam: the constructed-response sections. We hope that this Geometry Regents review guide was helpful. Proficient luck! What exactly are the New York State Regents Examinations? Learn all about these graduation requirements and what topics you'll have to take Regents in. Considering taking a unlike math Regents exam to fulfill your graduation requirements? Then check out our comprehensive review guides to Algebra 1 Regents and Algebra two Regents. In addition to a math Regents exam, you'll have to take a science Regents exam. Acquire most what to look on Chemical science Regents, World Scientific discipline Regents, and Living Environment Regents.
What'south the Format of the Geometry Regents Exam?
# of Questions Question Type Points per Question Partial Credit Given? Total Points Part I 24 (#i-24) Multiple choice 2 No 48 Part II vii (#25-31) Short response 2 Yes 14 Part III three (#32-34) Medium response 4 Yes 12 Part IV 1 (#35) Long response 6 Yes six TOTAL 35 — — — 80


What Exercise Geometry Regents Questions Await Like?
Multiple-Choice Sample Question (Part I)

$V={4/3}π(0.593)$
$V=(iv.189)(0.593)$
$V=2.484$Short-Response Sample Question (Function II)
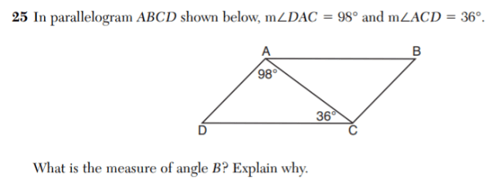
$180-134=46$
$∠ D=46°$
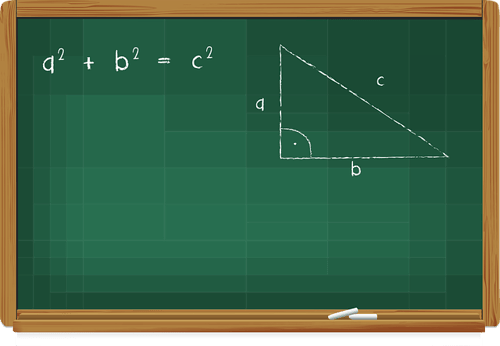
Medium-Response Sample Question (Role Three)

$V=390$
$9+ten^2=16$
$10^two=7$
$ten=√vii$
$x=2.6458$
$A=(one/2)(6)(two.6458)$
$A=(3)(two.6458)$
$A=7.9374$
$V=51.5931$
$V=441.5931$
$5=442$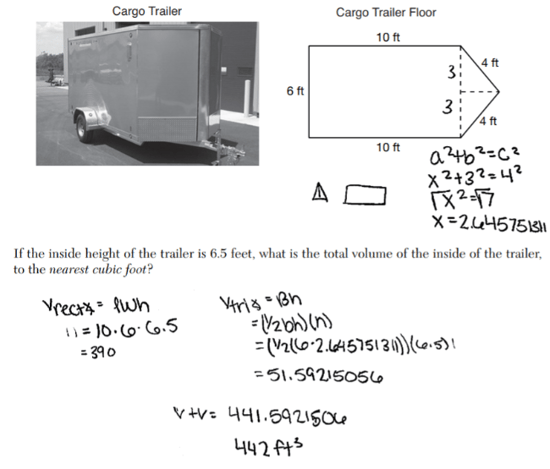

Long-Response Sample Question (Part IV)



Part 1
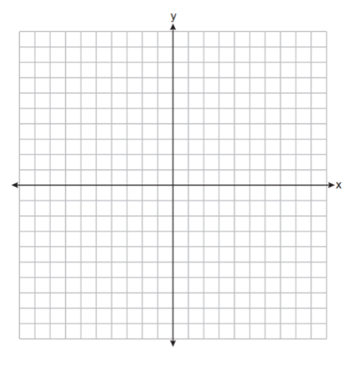
$√{-6^2+1^2}$
$√{36+ane}$
$√{37}$
$√{(-6+5)^ii+(-three-iii)^2}$
$√{-1^2+-6^2}$
$√{1+36}$
$√{37}$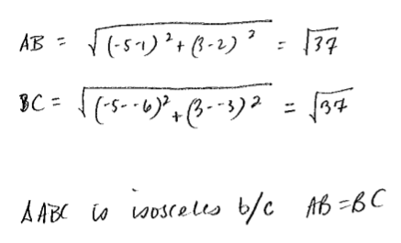
Role two
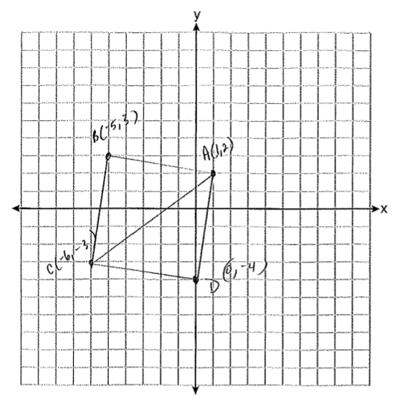
Function 3
$\ov {Ad}=√{-1^2+-6^2}$
$\ov {Advertizement}=√{1+36}$
$\ov {Advert}=√{37}$
$\ov {CD}=√{(0+6)^2+(-4+3)^2}$
$\ov {CD}=√{6^2+-1^2}$
$\ov {CD}=√{36+1}$
$\ov {CD}=√{37}$
$\Slope \of$ $\ov {AB}={ane}/{-6}$
$\Slope \of$ $\ov {AB}=-1/half dozen$
$\Slope \of$ $\ov {BC}=-six/{-6+5}$
$\Slope \of$ $\ov {BC}=-six/-ane$
$\Slope \of$ $\ov {BC}=6$

What Topics Does Geometry Regents Cover?
The Geometry Regents test covers pretty much everything that has to do with shapes in math. Major topics include the following (we've linked our relevant Sat/ACT math guides in case y'all need to review):
Domain Topics Percent of Test by Credit Congruence Experiment with transformations in the aeroplane 27-34% Understand congruence in terms of rigid motions Prove geometric theorems Brand geometric constructions Similarity, Correct Triangles, and Trigonometry Understand similarity in terms of similarity transformations 29-37% Bear witness theorems involving similarity Define trigonometric ratios and solve problems involving correct triangles Circles Understand and apply theorems about circles 2-8% Find arc lengths and areas of sectors of circles Expressing Geometric Backdrop with Equations Translate between the geometric clarification and the equation for a conic section 12-18% Use coordinates to prove simple geometric theorems algebraically Geometric Measurement & Dimensions Explain book formulas and use them to solve issues 2-viii% Visualize relationships between two-dimensional and three-dimensional objects Modeling with Geometry Apply geometric concepts in modeling situations 8-fifteen% 
How to Pass Geometry Regents: 5 Essential Tips
#ane: Have Real Practice Tests
#two: Review Major Topics Using Form Materials
#three: Become Help From Your Math Teacher (If Needed)
#4: Don't Spend Too Much Time on Part I
#v: Answer Every Question
Final Words: The Importance of Geometry Regents Review
What'south Next?

About the Author
Hannah received her MA in Japanese Studies from the Academy of Michigan and holds a available's degree from the University of Southern California. From 2013 to 2015, she taught English in Japan via the JET Plan. She is passionate almost education, writing, and travel.
collinsworthblit1942.blogspot.com
Source: https://blog.prepscholar.com/geometry-regents-review
0 Response to "Everything You Need to Know to Pass the Geometry Regents"
Post a Comment